Qui trovi un elenco completo delle formule di calcolo con i decibel divise per argomento.
Clicca la voce in elenco per iniziare a calcolare i decibel.
- Somma di decibel
- Differenza di decibel
- Calcolo del livello equivalente LAeq
- Conversione pressione sonora - decibel
- Calcolo della propagazione del suono
- Conversione potenza sonora - pressione sonora
- Conversione frequenza - lunghezza d'onda
- Calcolo del livello di esposizione al rumore
SOMMA DI DECIBEL
- Inserisci il livello di pressione sonora Lp di ogni sorgente (in decibel)
- Premi il pulsante "+" per aggiungere altre sorgenti
- Premi "INVIO" oppure pulsante "=" per calcolare il risultato
 Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di notare alcune peculiarità della fisica applicata all'acustica.
Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di notare alcune peculiarità della fisica applicata all'acustica.
Innanzitutto salta subito all'occhio che la somma di due sorgenti di pari intensità non equivale assolutamente al doppio
del livello di pressione sonora.
 In realtà la somma di due livelli identici comporta un aumento di soli 3 dB, qualunque sia
il valore in questione: (5 dB + 5 dB = 8 dB; 100 dB + 100 dB = 103 dB).
In realtà la somma di due livelli identici comporta un aumento di soli 3 dB, qualunque sia
il valore in questione: (5 dB + 5 dB = 8 dB; 100 dB + 100 dB = 103 dB).
La spiegazione risiede nel fatto che quando due sorgenti hanno uguale intensità, ciò che in effetti raddoppia è la pressione
sonora (p) e non il livello di pressione sonora (Lp). E siccome il livello Lp è sù per giù il logaritmo in base dieci
della pressione p, salta fuori un fattore aggiuntivo di 3 decibel per ogni raddoppio della pressione. La formula è la seguente:
 Una ulteriore conseguenza del fatto che le leggi dell'acustica siano governate dai logaritmi si riscontra quando si sommano
due lvelli di pressione sonora di cui uno molto superiore all'altro. Il risultato dell'addizione è pressoché identico al
termine maggiore. Di fatto è sufficiente che i due addendi si discostino di 10 decibel affinchè il termine più piccolo
diventi ininfluente ai fini della somma.
Una ulteriore conseguenza del fatto che le leggi dell'acustica siano governate dai logaritmi si riscontra quando si sommano
due lvelli di pressione sonora di cui uno molto superiore all'altro. Il risultato dell'addizione è pressoché identico al
termine maggiore. Di fatto è sufficiente che i due addendi si discostino di 10 decibel affinchè il termine più piccolo
diventi ininfluente ai fini della somma.


DIFFERENZA DI DECIBEL
- Inserisci il livello di pressione sonora Lp di ogni sorgente (in decibel)
- Premi il pulsante "-" per aggiungere altre sorgenti
- Premi "INVIO" oppure pulsante "=" per calcolare il risultato
 Per la differenza di decibel la spiegazione teorica è la stessa di sopra riguardante la somma.
Per la differenza di decibel la spiegazione teorica è la stessa di sopra riguardante la somma.
LIVELLO EQUIVALENTE di PRESSIONE SONORA
- Inserisci il livello di pressione Lp sonora di ogni intervallo (in decibel)
- Inserisci la durata T di ogni intervallo (tutte in ore o tutte in minuti...)
- Premi il pulsante "+" per aggiungere altri contributi
- Premi "INVIO" oppure pulsante "=" per calcolare il risultato
 Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di comprendere il significato del Livello equivalente continuo ponderato LAeq.
Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di comprendere il significato del Livello equivalente continuo ponderato LAeq.
Il Livello equivalente è la media integrata nel tempo del livello di pressione sonora. Definisce dunque un valore univoco
descrittivo della rumorosità complessiva. Diversamente invece il Livello di pressione sonora è indicativo della rumorosità
istante per istante. Dunque il primo, all'aumentare del tempo di misura, tende a diventare costante; il secondo è in continuo
mutamento. Nella seguente figura, che mostra la Time History di una comune misurazione fonometrica, tutto ciò può essere
facilmente visualizzato. La Time History è un grafico che rappresenta l'andamento del livello di rumore nel tempo. La linea
blue rappresenta il livello di pressione sonora istantaneo, la linea rossa rappresenta il Livello equivalente.
 Supponiamo di voler caratterizzare la rumorosità di un determinato ambiente di indagine. Il rumore di certo non avrà sempre
costantemente la stessa intensità. Immaginaniamo però che in questo luogo vi siano tre lavorazioni principali molto rumorose
e che si susseguano. Come visto nella pagina relativa alla somma di livelli di pressione sonora, un rumore molto più intenso di tutti
gli altri presenti equivale alla intensità complessiva. Dunque si può dedurre che la rumorosità complessiva dell'ambiente di
indagine sia data esclusivamente prima da una lavorazione, poi dalla successiva ed infine dall'ultima lavorazione.
Nel caso non si potesse effettuare una rilevazione fonometrica durante tutta la giornata lavorativa, è possibile misurare alcuni
minuti di ciascuna delle tre fasi di lavorazione. Otterremmo tre livelli di pressione Lp1, Lp2, Lp3. Conoscendo le durate T1, T2, T3
delle lavorazioni, per mezzo della formula seguente (su cui si basa l'utility di calcolo soprastante), otterremo lo stesso risultato.
Supponiamo di voler caratterizzare la rumorosità di un determinato ambiente di indagine. Il rumore di certo non avrà sempre
costantemente la stessa intensità. Immaginaniamo però che in questo luogo vi siano tre lavorazioni principali molto rumorose
e che si susseguano. Come visto nella pagina relativa alla somma di livelli di pressione sonora, un rumore molto più intenso di tutti
gli altri presenti equivale alla intensità complessiva. Dunque si può dedurre che la rumorosità complessiva dell'ambiente di
indagine sia data esclusivamente prima da una lavorazione, poi dalla successiva ed infine dall'ultima lavorazione.
Nel caso non si potesse effettuare una rilevazione fonometrica durante tutta la giornata lavorativa, è possibile misurare alcuni
minuti di ciascuna delle tre fasi di lavorazione. Otterremmo tre livelli di pressione Lp1, Lp2, Lp3. Conoscendo le durate T1, T2, T3
delle lavorazioni, per mezzo della formula seguente (su cui si basa l'utility di calcolo soprastante), otterremo lo stesso risultato.
 Una peculiarità delle leggi dell'acustica, dovuta alla presenza dei logaritmi all'interno delle formule, si riscopre nel
fatto che singoli eventi di elevata rumorosità, anche se di durata ridotta rispetto al resto del tempo di misura, diventano
decidivi ai fini del valore finale del Livello equivalente. In poche parole una intera misura a bassi livelli di rumore può
essere facilmente sfalsata da un singolo evento molto rumoroso, poichè il livello equivalente ne risente sensibilmente.
Una peculiarità delle leggi dell'acustica, dovuta alla presenza dei logaritmi all'interno delle formule, si riscopre nel
fatto che singoli eventi di elevata rumorosità, anche se di durata ridotta rispetto al resto del tempo di misura, diventano
decidivi ai fini del valore finale del Livello equivalente. In poche parole una intera misura a bassi livelli di rumore può
essere facilmente sfalsata da un singolo evento molto rumoroso, poichè il livello equivalente ne risente sensibilmente.

CONVERSIONE PRESSIONE SONORA - DECIBEL
- Inserisci la pressione sonora p (in microPascal)
- Premi "INVIO" oppure pulsante "=" per convertire in livello di pressione sonora Lp (in decibel)
- E viceversa...
Pressione sonora → livello di pressione
Livello di pressione → pressione sonora
 Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di convertire i decibel in pressione e viceversa.
Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di convertire i decibel in pressione e viceversa.
Quando si parla di rumore, si pensa direttamente ai decibel, cioè l'unità di misura dell'intensità di un segnale sonoro.
In realtà però il decibel non è altro che un artificio tecnico per rappresentare l'intera gamma di suoni (dai più forti ai
più deboli) su una scala molto più corta e facilmente memorizzabile. Infatti, il vero indicatore dell'intensità di un suono
è la pressione. Del resto, un'onda sonora è essenzialmente una variazione della pressione dell'aria ocomunque del mezzo
elastico entro cui essa si propaga.

Un semplice esempio per capire il perchè di questo artificio di conversione: è molto più semplice memorizzare che un aereo
produce 130 dB mentre il fruscio delle foglie 25 dB, anzichè memorizzare che un aereo produce 63,25 Pa ed il fruscio delle
foglie 356 µPa. Inoltre in tal modo si riduce notevolmente il campo di misura in cui ricadono i suoni più comuni a cui
siamo abituati. Dal suono più lieve, come il fruscio delle foglie, al suono più forte che possiamo immaginare, come un aereo
in decollo, sulla scala dei decibel troviamo solamente 100 decibel di differenza. La totalità dei suoni che possiamo percepire
ricade in questo intervallo. Se invece ragionassimo in termini di pressione allora andremmo da 0,000365 a 63,25 Pascal.
L'intervallo diventa evidentemente troppo esteso e difficilmente memorizzabile come ordine di grandezza. A tutto ciò
ovviamente si aggiunge la comodità di ragionare solo con numeri interi.

CALCOLO DELLA PROPAGAZIONE DEL SUONO
- Inserisci il livello di pressione sonora noto Lp (in decibel)
- Inserisci la distanza d1 nota (in metri)
- Inserisci la distanza d2 a cui calcolare (in metri)
- Premi "INVIO" oppure pulsante "=" per calcolare il livello di pressione sonora (in decibel)
 Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di calcolare in che modo si propaga il rumore si una sorgente puntiforme nello spazio.
Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di calcolare in che modo si propaga il rumore si una sorgente puntiforme nello spazio.
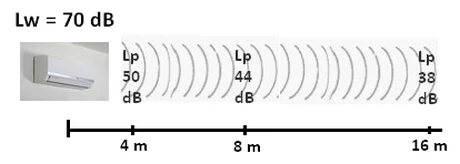
Innanzitutto occorre spiegare la differenza tra Livello di pressione Lp e Livello di potenza Lw. Il livello
di potenza sonora indica la sonorità intrinseca di una sorgente ed è un valore univoco. Diversamente il livello di pressione
sonora indica la sonorità di una sorgente nei vari punti dello spazio per cui dipende dalla distanza. Man mano che ci si allontana
dalla sorgente il livello di pressione sonora diminuisce comprensibilmente mentre il livello di potenza sonora rimane sempre
il medesimo perchè è una caratteristica oggettiva della sorgente.

La conversione da livello di potenza a livello di pressione è molto utile nel momento in cui si desidera prevedere il rumore prodotto da una determinata apparecchiatura ad una certa distanza a partire dai dati forniti dal costruttore. Solitamente, infatti la casa produttrice fornisce il livello di potenza del macchinario, calcolato in laboratorio con apposite prove di emissione sonora. Nella seconda utility di calcolo di questa pagina si nota come, ai fini della conversione da Lw a Lp, sia necessario il fattore di direttività Q. Esso dipende dal posizionamento della sorgente rispetto ai piani di appoggio. E' facile intuire come l'emissività sonora di una sorgente sia molto più forte se essa è posta in una spigolo piuttosto che su un piano orizzontale. Nel primo caso, infatti, la fetta di spazio attraverso cui il rumore si può propagare è molto più piccola dunque l'onda di propagazione molto più concentrata.
Utilizzando la prima utility di calcolo di questa pagina si può facilmente notare come il livello di pressione sonora di una sorgente sonora diminuisce di 6 decibel ad ogni raddoppio della distanza. Per cui se un condizionatore emette 66 decibel a 3 metri se ne percepiranno 60 a 6 metri e 54 a 12 metri e così via...
CONVERSIONE POTENZA SONORA - PRESSIONE SONORA
- Inserisci la potenza sonora Lw (in decibel)
- Inserisci la direttività Q della sorgente (vedi immagine sotto)
- Inserisci la distanza d (in metri)
- Premi "INVIO" oppure pulsante "=" per convertire in livello di pressione sonora (in decibel)
- E viceversa...
Potenza sonora → pressione sonora
Pressione sonora → potenza sonora
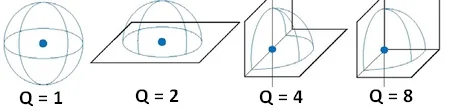
Indice di direttività della propagazione del suono
 Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di calcolare in che modo si propaga il rumore si una sorgente puntiforme nello spazio.
Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di calcolare in che modo si propaga il rumore si una sorgente puntiforme nello spazio.
Innanzitutto occorre spiegare la differenza tra Livello di pressione Lp e Livello di potenza Lw. Il livello
di potenza sonora indica la sonorità intrinseca di una sorgente ed è un valore univoco. Diversamente il livello di pressione
sonora indica la sonorità di una sorgente nei vari punti dello spazio per cui dipende dalla distanza. Man mano che ci si allontana
dalla sorgente il livello di pressione sonora diminuisce comprensibilmente mentre il livello di potenza sonora rimane sempre
il medesimo perchè è una caratteristica oggettiva della sorgente.

La conversione da livello di potenza a livello di pressione è molto utile nel momento in cui si desidera prevedere il rumore
prodotto da una determinata apparecchiatura ad una certa distanza a partire dai dati forniti dal costruttore. Solitamente, infatti
la casa produttrice fornisce il livello di potenza del macchinario, calcolato in laboratorio con apposite prove di emissione
sonora. Nella seconda utility di calcolo di questa pagina si nota come, ai fini della conversione da Lw a Lp, sia necessario
il fattore di direttività Q. Esso dipende dal posizionamento della sorgente rispetto ai piani di appoggio. E' facile intuire come
l'emissività sonora di una sorgente sia molto più forte se essa è posta in una spigolo piuttosto che su un piano orizzontale.
Nel primo caso, infatti, la fetta di spazio attraverso cui il rumore si può propagare è molto più piccola dunque l'onda di
propagazione molto più concentrata.
Utilizzando la prima utility di calcolo di questa pagina si può facilmente notare come il livello di pressione sonora di una
sorgente sonora diminuisce di 6 decibel ad ogni raddoppio della distanza. Per cui se un condizionatore emette 66 decibel a 3 metri
se ne percepiranno 60 a 6 metri e 54 a 12 metri e così via...

CONVERSIONE FREQUENZA - LUNGHEZZA D'ONDA
- Inserisci la temperatura dell'aria t (in °C)
- Inserisci la frequenza sonora F (in Hertz)
- Premi "INVIO" oppure pulsante "=" per convertire in lunghezza d'onda λ (in metri)
- E viceversa...
Frequenza sonora → lunghezza d'onda
Lunghezza d'onda → frequenza sonora
 Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di convertire la frequenza in lunghezza d'onda e viceversa. Le due grandezze, infatti, sono strettamente
correlate tra di loro. Sono inversamente proporzionali ed il loro prodotto è pari alla velocità del suono caratteristica del
mezzo elastico di propagazione. Nel caso più comune dell'aria, la velocità di propagazione c è pari a 331 metri al secondo circa.
Con questo piccolo calcolo è possibile notare come a frequenze molto alte corrispondano lunghezze d'onda molto basse e viceversa.
Pertanto sarà facile ricordare che un suono molto acuto (frequenza alta) ha un'onda con un gran numero di oscillazioni ravvicinate.
Al contrario un suono molto grave (frequenza bassa) ha un'onda con poche e distanti oscillazioni.
Questa semplice utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di convertire la frequenza in lunghezza d'onda e viceversa. Le due grandezze, infatti, sono strettamente
correlate tra di loro. Sono inversamente proporzionali ed il loro prodotto è pari alla velocità del suono caratteristica del
mezzo elastico di propagazione. Nel caso più comune dell'aria, la velocità di propagazione c è pari a 331 metri al secondo circa.
Con questo piccolo calcolo è possibile notare come a frequenze molto alte corrispondano lunghezze d'onda molto basse e viceversa.
Pertanto sarà facile ricordare che un suono molto acuto (frequenza alta) ha un'onda con un gran numero di oscillazioni ravvicinate.
Al contrario un suono molto grave (frequenza bassa) ha un'onda con poche e distanti oscillazioni.

CALCOLO DEL LIVELLO DI ESPOSIZIONE AL RUMORE
- Inserisci il livello di pressione sonora Lp di ogni compito (in decibel)
- Inserisci la durata T di ogni compito (in minuti)
- Premi il pulsante "+" per aggiungere altri compiti
- Premi "INVIO" oppure pulsante "=" per calcolare il risultato
 Questa complessa utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di calcolare, a meno dell'incertezza di misura, il livello di esposizione giornaliera al rumore partendo dalle
misure relative a ciascun compito che compone la mansione. Secondo la nuova NORMA UNI 9432:2011 e 9612:2011, per ciascun
compito si devono effettuare tre misure al fine di definire quanto più compiutamente possibile il livello sonoro caratteristico
dei vari compiti. Se le tre misure differiscono di oltre 3 dB non sono valide per cui occorre effettuare nuove rilevazioni fonometriche.
L'utility non prevede il calcolo dell'incertezza di misura poichè essa dipende da numerosi fattori legati alla modalità di indagine e di misura.
Questa complessa utility di calcolo, molto spesso ricercata da chi opera nel settore dell'acustica,
ci permette di calcolare, a meno dell'incertezza di misura, il livello di esposizione giornaliera al rumore partendo dalle
misure relative a ciascun compito che compone la mansione. Secondo la nuova NORMA UNI 9432:2011 e 9612:2011, per ciascun
compito si devono effettuare tre misure al fine di definire quanto più compiutamente possibile il livello sonoro caratteristico
dei vari compiti. Se le tre misure differiscono di oltre 3 dB non sono valide per cui occorre effettuare nuove rilevazioni fonometriche.
L'utility non prevede il calcolo dell'incertezza di misura poichè essa dipende da numerosi fattori legati alla modalità di indagine e di misura.
